(海松波画)
作者:手塚桐鳳
備考:紙箱入

※画像を押すと拡大できます。
濃緑色の幹が多数、枝分かれしたものみたいです。
見た目が松の枝葉に似ているところからの名前でしょうか。
昔は朝廷への献上品だったようです。
この海松を模様化したものが「海松模様」で、
平安時代からあった文様のようです。
波や海藻を配したものが多いのだとか。
海松色というものもあるそうで、
Webで表示すると
■■■■■海松色■■■■■
のようになるみたいです。
海松に関する歌は『万葉集』にもあるそうで、
神風の 伊勢の海の 朝なぎに 来寄る深海松
夕なぎに 来寄る股海松 深海松の 深めし我れを
俣海松の また行き帰り 妻と言はじとかも 思ほせる君
(作者不詳 巻13-3301)
など5首(全部長歌)があるようです。
作者:西村徳泉
備考:紙箱入

※画像を押すと拡大できます。
共蓋の振出の場合は、
茶入・水滴(硯石に水を注ぎ入れる器)などに、
使うことも可能なようです。
青磁・祥瑞・宋胡録などの振出で、
このような使い方もできるのではないでしょうか。
作者:昌山(茶碗)
備考:紙箱入

※画像を押すと拡大できます。
金平糖という言葉は、オランダ語でお菓子を表わす
「コンフェイト」から来ているそうです。
日本に入ってきたのは、1569年にポルトガルの宣教師が、
織田信長に献上したのが始まりみたいです。
■金平糖の作り方
1.氷砂糖に水を加えて煮詰め、蜜をつくる。
2.回転鍋(銅鑼)を熱しながら、金平糖の核となるケシ粒(ザラメ糖)を入れる。
3.ケシ粒に熱い蜜を少量ずつかけ、
回転させながら目的の大きさと凹凸状の突起ができあがるまで、
1週間〜2週間以上かけて粒をゆっくり成長させていく。
■金平糖の突起
この特徴的な突起がなぜ、またいくつ形成されるのかについての定説は、
現在になっても、まだないのだそうです。
蔵本・シバシンスキー方程式により、定式化が試みられていたり、
寺田寅彦が「金平糖の角の研究」をしたようです。
綺麗に突起を成長させるための必要条件は、
1.全ての粒子の表面が糖蜜の薄い層をまとった状態にあること。
2.成長した結晶粒が攪拌によって均等に混ざり合い、サイズ毎に分離しないこと。
だそうです。
■乱流
以下、完全に物理学の世界になりますが、
蔵本・シバシンスキー方程式を出すために、
まず「乱流」の説明からしようかと思います。
乱流というのは、時間・空間的な乱れが持続する状態を言うそうで、
「水の流れ」がその代表だそうです。
1883年、オズボーン・レイノルズは、水槽で観測実験をして、
1885年、ナヴィエ・ストークス方程式が発表されるようです。
1925年、ルートヴィヒ・プラントルが、気体で似たような感じになることを
理論的に解析したみたいです。
1935年、テイラーが、統計学的に理論解析できるようにしたそうです。
これで「実験」「理論」が出そろい、コンピューターが登場すると、
「コンピューターによるシミュレーション」が本格化するそうです。
1960年後半、ナヴィエ・ストークス方程式の乱流解というものを
シミュレートする研究が始まるようです。
ナヴィエ・ストークス方程式
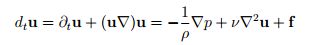
(※「u」は連続体の速度場、「p」は圧力、「f」は外力、
「ρ」は密度、「ν」は動粘性係数だそうです。)
■蔵本・シバシンスキー方程式
シミュレーション研究の進歩で、
乱流の主な研究対象であった流体系以外でも、
様々な偏微分方程式について、
乱流解が存在することが明らかになってきたそうです。
例えば、先に出したナヴィエ・ストークス方程式の場合、
「レイノルズ数」という値を変化させることで、乱流(非線形性)を
表わすようになるのだとか。
中でも、複数の非線形偏微分方程式として物理界では有名な式が、
複素ギンズブルグ-ランダウ方程式だそうです。
これで、乱流の空間二次元の振る舞いが、わかるようになるみたいです。
(位相乱流や振幅乱流の他、標的パターンや回転らせん波のパターンが現れるのだとか。)
ちなみに、元々のギンズブルグ-ランダウ理論は、
1950年にロシアで発表された超伝導を説明する現象論だそうです。
複素ギンズブルグ-ランダウ方程式
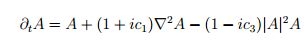
(※「A」は時間「t」 と空間 x の複素関数で、理想的な自励振動場を表わすようで、
「c1」は線形散逸のパラメータ、「c3」は非線形散逸のパラメータ)
そして、この複素ギンズブルグ-ランダウ方程式を、
簡単に(位相成分ψを近似)したのが、
蔵本・シバシンスキー方程式だそうです。
蔵本・シバシンスキー方程式
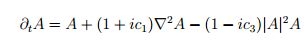
この式は、炎の表面の振る舞いを表わしたものだそうで、
三次元の乱流の振る舞いが、わかるのだとか。
金平糖の角も、この近似式によって、大まかにわかるみたいです。
作者:桐鳳
価格:8,000円
備考:紙箱入
/振出は、桐鳳の作ではありません。

※画像を押すと拡大できます。
いくつか挙げてみようと思います。
| 茶箱名 | 振出名 | 大きさ |
|---|---|---|
| 利休好 菊置上茶箱 | 赤楽振出 | 高7.6cm×口径2.0cm×底径5.1cm |
| 玄々斎好 裂蒔絵茶箱 | 白釉口四方振出(保全作) | 高9.4cm×口径2.7cm |
| 玄々斎好 春秋七草茶箱 | 織部振出(慶入作) | 高10.6cm×口径2.8cm×底径3.2cm |
| 玄々斎好 匙鉋目茶箱 | 楽茄子形振出(旦入作) | 高7.2cm×口径2.3cm×底径5.6cm |
| 淡々斎好 雪月花茶箱 | 龍文交趾写振出(即全作) | 高8.2cm×口径3.4cm |
作者:御室窯(振出・茶巾筒)
備考:木箱入

※画像を押すと拡大できます。
仁和寺宮の許しで御室仁和寺門前にて御室窯を開いたそうです。
江戸末期、旧地に永楽和全が一時期新しく窯を築き
「おむろ」印を用いるようになるとか。







